Linked List Cycle

Problem Description

We have given a head of a linked list and asked return a boolean value whether the linked list has a cycle or not.
For full explanation: Linked List Cycle

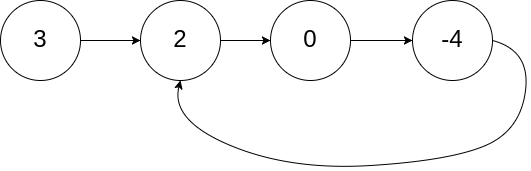
Here is the representation of a linked list cycle.
There is a cycle between 2 and -4 nodes as show below

Intuition

The solution comes from Floyd's Cycle Detection algorithm also known as Hare-Tortoise algorithm.

Pseudocode as follows:

1. initialize slow and fast pointers (by the head of the linked list)
2. move slow pointer by one node
3. move fast pointer by two nodes
4. if both pointers meet at some node then cycle exists, if fast pointer meets end of the linked list then cycle does not exist

Let's analyze it step by step:

1. slow at 3, fast at 3
2. move slow pointer by one, slow at 2; move fast pointer by two, fast at 0
3. move slow pointer by one, slow at 0; move fast pointer by two, fast at 2
4. move slow pointer by one, slow at -4; move fast pointer by two, fast at -4 -> return.

both meets at -4 then cycle is exists.

Solution

class ListNode{
  int val;
  ListNode next;
  ListNode(int x) {
    val = x;
    next = null;
  }
}

public boolean hasCycle(ListNode head) {
  if(head == null) return false;
  ListNode slow = head, fast = head;
  
  while(fast != null && fast.next != null){
    slow = slow.next;
    fast = fast.next.next;
    if(slow == fast) return true;
  }

  return false;
}